
Les géodésiques de la sphère.
Dans le plan, la longueur d'une courbe s'obtient en approchant la courbe par une ligne polygonale, donc formée de segments de droites.
Sur la sphère, on peut définir la longueur d'une courbe en approchant la courbe par une ligne polygonale. Mais puisqu'on est sur la sphère, autant considérer cette ligne polygonale sur la sphère elle-même, donc formée d'arcs, et tant qu'à faire, d'arcs de grands cercles, plutôt que de sortir de la sphère, d'aller dans l'espace, et de prendre encore des segments de droites.

Dans ces conditions, l'inégalité triangulaire sur les arcs de grands cercles prouve que la longueur de l'arc de grand cercle AB est plus courte que celle de toute "ligne polygonale" dont les extrémités sont A et B. Donc aussi que celles qui approchent la longueur de la courbe à moins de e.
On a donc :
Donc aussi :
Puisque ceci est vrai pour tout e > 0, on en tire : AB < courbe et donc l'arc de grand cercle est bien la géodésique qui joint A à B.
Reste :
S'assurer de l'inégalité
triangulaire. C'est à peu près évident quand on
la regarde avec les angles au centre.

Il s'agit de prouver que dans un trièdre, un des trois angles est toujours inférieur à la somme des deux autres, l'égalité n'ayant lieu que si les trois angles sont dans un même plan (et que le trièdre n'en est plus un).
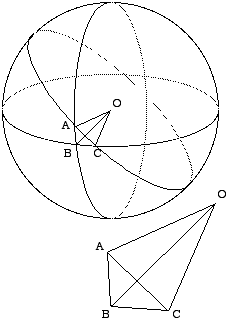
Voir s'il peut exister une autre courbe sur la sphère, qui ait
exactement même longueur que l'arc de grand cercle ayant
mêmes extrémités.
Supposons en effet qu'il existe une telle courbe (donc de même longueur que le grand cercle AB) dont un point C soit hors du grand cercle AB (s'il n'existe pas de tel point C, c'est que la géodésique est le grand cercle AB).
La longueur de cette courbe est la somme des longueurs de ses bouts allant de A à C et de C à B. Pour aller de A à C, la longueur la plus courte est celle du grand cercle AC, donc le bout allant de A à C a pour longueur celle du grand cercle AC.
De même, le bout allant de C à B a même longueur que le grand cercle CB. Et donc la longueur totale de la courbe, égale à celle du grand cercle AB, est égale à la somme des grands cercles AC et CB. Sur les grands cercles, on aura :
ce qui n'est pas possible pour C en dehors de AB. Il ne peut donc exister sur la sphère de courbe autre que le grand cercle AB qui ait même longueur que lui : le grand cercle AB est la géodésique qui joint A à B.
S'assurer que la longueur de courbe ainsi définie est la
même que celle qu'on obtient avec des segments (juste à titre de satisfaction intellectuelle, parce
que ... si on dit qu'on est sur la sphère, pourquoi se
considérerait-on dans l'espace à 3D ? C'est d'ailleurs
ce qui me paraît intéressant dans le Flatland d'Abbott :
voir le plan de l'intérieur).
Il est clair que le problème est celui de la définition de la longueur d'une courbe : qu'est-ce que la longueur d'une courbe ? Par exemple :
Il est clair, parce que le segment de droite est le plus court chemin entre deux points, que tout polygone inscrit dans le cercle est de longueur plus courte que celle du cercle. Mais pourquoi un polygone circonscrit au cercle a-t-il une longueur supérieure à celle du cercle ?
Il serait satisfaisant que la notion de courbe rectifiable puisse se "prolonger" de la sphère à l'espace, et qu'on ne soit pas obligé d'avoir deux notions différentes pour la même courbe, suivant qu'on la voit dans la sphère ou dans l'espace. S'il me paraît presqu'évident qu'une courbe "rectifiable" par des arcs de grands cercles l'est aussi par des segments, il m'est moins immédiat qu'une courbe rectifiable le soit encore par des arcs de grands cercles (en fait, c'est exactement l'inverse, il n'y a donc rien d'évident). C'est le même problème, ou presque quand on passe du plan à l'espace : est-ce qu'une courbe plane a la même longueur dans son plan et dans l'espace ; est-ce que les courbes planes rectifiables sont les mêmes quand on les regarde dans leur plan ou dans l'espace ?