Géométrie sur la sphère : les droites sont les grands cercles.
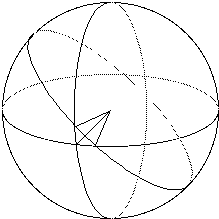
géométrie : géométrie = mesure de la terre ? mézalor, étude de la terre !
Si on reprend la
définition de la droite, on a en
particulier l'idée de ne dévier ni à droite ni
à gauche. (La ligne
droite est celle qui, étant menée d'un point à
un autre, ne se tourne ni à droite ni à gauche et qui
est la plus courte que l'on puisse mener entre ces deux
points.) Quand on cherche les "géodésiques" de
la sphère, on trouve les
"grands-cercles" (c'est-à-dire, par exemple, les
méridiens, l'équateur, mais surtout pas les
"parallèles"). Si on essaie de "prolonger" un minuscule
segment (sur une feuille) en restant à la surface de la terre,
et sans dévier ni à droite ni à gauche, on
obtiendra bien un "grand-cercle".
|
Géométrie sur la sphère : les droites sont les grands cercles. |
|
Il y a des différences avec la géométrie euclidienne.
D'abord, par deux points il ne passe pas toujours une et une seule droite : deux points diamétralement opposés sont à l'intersection d'une infinité de grands cercles (c'est typiquement le cas du pôle nord et du pôle sud qui sont sur tous les méridiens).
Par contre, si les deux points ne sont pas diamétralement opposés, ni confondus, ils déterminent avec le centre de la sphère un plan unique dont l'intersection avec la sphère donne l'unique grand cercle passant par ces deux points.
Si on veut pouvoir disposer de l'axiome classique "par deux points il passe une droite et une seule", on se contentera d'une demi-sphère, dont on ne garde que la moitié du cercle frontière, avec une seule des extrémités de ce grand-cercle. On sera alors assuré qu'il n'y a plus moyen d'avoir deux points diamétralement opposés.
Dans les différences notables avec la géométrie classique ...
Le parallélisme de deux grands-cercles, c'est leur égalité : deux grands-cercles différents se coupent toujours en deux points diamétralement opposés, donc deux grands-cercles qui ne se rencontrent pas, ça n'existe pas. La notion de parallélisme n'a donc aucun intérêt sur la sphère (pourquoi appeler "parallèle" ce qui s'appelle déjà "égal" ?). On est dans une situation de géométrie non-euclidienne, ici elliptique.
La somme des angles d'un triangle n'est donc plus 180° ; elle est toujours > 180°, mais surtout, elle est variable d'un triangle à un autre.
Exemple :
- je pars du pôle nord en suivant le méridien de Greenwich (0°), jusqu'à atteindre l'équateur ;
- je reste sur l'équateur jusqu'à atteindre le méridien 90°-est (ou x°) ;
- je remonte jusqu'au pôle nord en suivant ce méridien.
Comme les méridiens et l'équateur sont perpendiculaires, on a deux angles de 90° ; le troisième angle est de 90° (ou de x°) ; donc la somme des angles de ce triangle (gigantesque, deux côtés mesurent dix mille kilomètres de long) est de 90 + 90 + 90 (ou 90 + 90 + x), donc de 270° (ou 180° + x°). On a ainsi toute une famille de triangles dont la somme des angles varie de presque 180° (si x est presque nul) à 180 + 360 = 540° (si x est proche de 360°, c'est-à-dire si on a parcouru presque tout l'équateur). La somme des angles d'un triangle n'est pas constante (ce qui serait la situation en géométrie euclidienne). Au passage, pour x = 90°, on a un exemple de triangle équilatéral dont les trois angles sont droits.
Si on reprend l'exemple du triangle équilatéral dont les côtés mesurent 10 000 km, et dont les trois angles valent 90°, il est clair qu'on ne peut pas lui appliquer le théorème de Pythagore. D'ailleurs, la version grecque du théorème de Pythagore voulait que l'on construise un carré sur chaque côté du triangle ...