Géométries non-euclidiennes :
diagrammes d'Escher (cercles limites) ou de ce type ; donner
plusieurs modèles de géometries
non-euclidiennes.
Il est bien difficile de donner une définition de la
droite. En dehors de toute
considération politique, il y a tout de même plusieurs
points de vue qui donnent lieu à plusieurs types de
définition. En géométrie affine, on peut retenir
l'idée d'"alignement de points". (En géométrie
métrique, ce serait l'idée de "plus court chemin" qui
l'emporterait.)
|
A propos d'alignement, on peut s'aider de
certaines oeuvres d'Escher, sur lesquelles, il
s'avère qu'on pourrait aussi avoir un point de vue
métrique.
Par exemple, ci-contre, Escher remplit le
plan avec des "pavés" en forme d'anges et de
démons. Le remplissage est "régulier", aucune
pièce n'en chevauche une autre, aucun "jour" n'est
laissé entre deux pièces.
En fait les pièces sont
alignées, les alignements s'obtenant en traversant
tantôt une pièce en forme d'ange, tantôt
une pièce en forme de démon. Mais bien
sûr, il y a d'autres alignements qui apparaissent, en
biais (on les devine plutôt qu'on ne les voit, car le
dessin n'est pas de taille assez grande ; voir
ci-dessous).
|

|




Escher a
utilisé ce qui semble être les mêmes pièces
(anges et démons) pour faire ce qu'il appelle une "limite
circulaire". Voir le
modèle de géométrie hyperbolique dans le disque
d'Escher. La droite AB y est soit un
diamètre du cercle horizon passant par A et B, soit la trace
du cercle passant par A et B et qui coupe le cercle horizon
perpendiculairement.
Un autre modèle de géométrie
hyperbolique : le demi-plan de Poincaré.
|
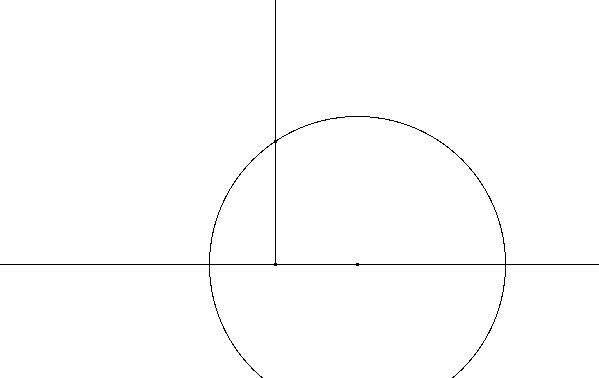
La droite AB est :
- soit une demi-droite perpendiculaire
à l'horizon, et passant par A et B,
- soit la trace du cercle passant par A
et B et qui est centré sur l'horizon.
Recette de la construction de la droite
AB (dans le cas du demi-cercle) : le centre du demi-cercle
voulu est l'intersection de l'horizon avec la
médiatrice des points A et B.
|
|
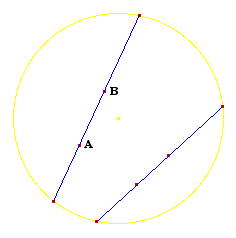
Encore un autre modèle de
géométrie hyperbolique, dans le disque :
|
La droite AB est tout simplement la trace
dans le disque de la droite euclidienne AB.
|
|
On peut aussi donner un modèle de
"géométrie elliptique" dans le disque.
|
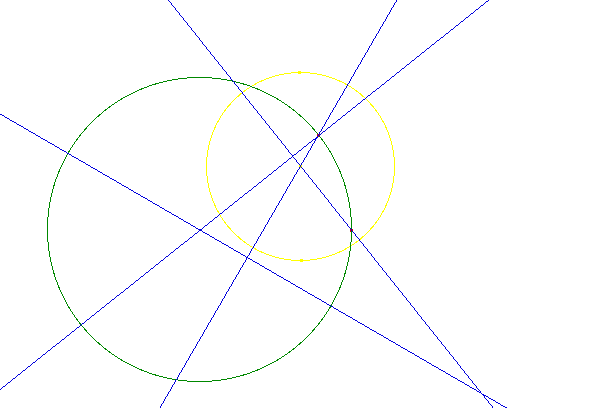
La droite AB est :
- soit un diamètre du cercle
horizon (en jaune) passant par A et B,
- soit la trace du cercle (en vert)
passant par A et B et qui intercepte un diamètre
du cercle horizon.
|

|
Recette de la construction de la droite AB (dans
le cas de la trace de cercle) :
|
Etant donné un point du cercle
horizon, et son symétrique par rapport au centre O,
ces deux points diamétralement opposés et le
point A déterminent un cercle (son centre H :
intersection des médiatrices des côtés
du triangle). Construire de ce centre la droite
perpendiculaire au rayon OA.
|

|
|
Recommencer à partir du point B.
Le centre du cercle cherché sera le point
d'intersection de ces deux droites (respectivement
perpendiculaires à OA et à OB).
|
|
Il y a donc trois types de
"géométrie plane" :
- la géométrie euclidienne,
- la géométrie
hyperbolique,
- la géométrie elliptique.
En géométrie euclidienne, la somme
des angles d'un triangle est 180°, et (ce qui est
équivalent) on dispose de l'axiome des parallèles :
étant donnés un point et une droite ne passant pas par
ce point, il existe une et une seule droite qui ne rencontre pas
celle-ci et qui passe par celui-là.
En géométrie hyperbolique, la somme
des angles d'un triangle est < 180°, et (ce qui est
équivalent) on dispose de l'axiome : étant
donnés un point et une droite ne passant pas par ce point, il
existe au moins deux droites (en fait, une infinité) qui ne
rencontrent pas celle-ci et qui passe par celui-là.
En géométrie elliptique, la somme
des angles d'un triangle est > 180°, et (ce qui est
équivalent) on dispose de l'axiome : étant
donnés un point et une droite ne passant pas par ce point, il
n'existe aucune droite qui rencontre celle-ci et qui passe par
celui-là. Un
assez bon exemple d'une telle géométrie est
donné par la sphère.
retour au
sommaire









